Chapter 2 线性混合模型

2.1 案例1

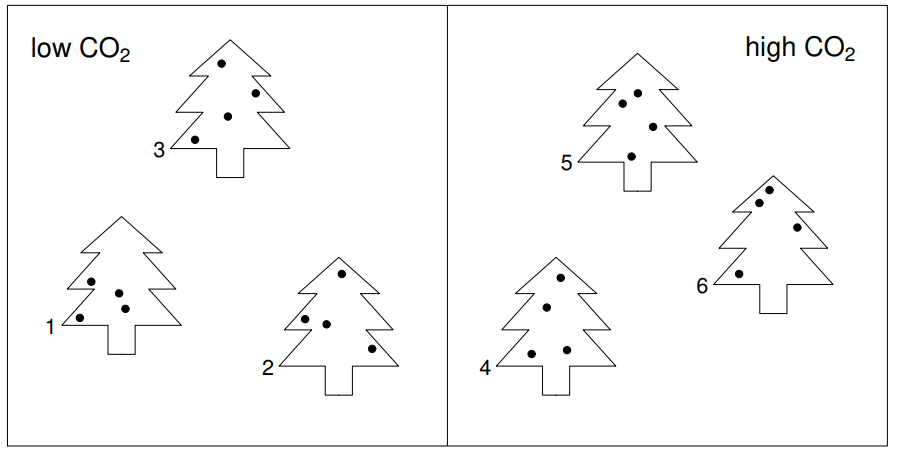
两组CO2实验，高CO2浓度和低CO2浓度。每组3棵树（tree）、每棵树测4片叶子的气孔面积（area）。

问题：CO2对气孔导度的影响

2.1.1 错误的方法，固定效应模型

library(JOPSbook)
library(gamair)
library(magrittr)
library(data.table)

data("stomata")
stomata %<>% data.table()

summary(stomata)

#>       area        CO2    tree 
#>  Min.   :0.8753   1:12   1:4  
#>  1st Qu.:1.5396   2:12   2:4  
#>  Median :2.0166          3:4  
#>  Mean   :2.0679          4:4  
#>  3rd Qu.:2.7600          5:4  
#>  Max.   :3.1149          6:4

print(stomata)

#>          area CO2 tree
#>  1: 1.6055739   1    1
#>  2: 1.6300711   1    1
#>  3: 1.5391189   1    1
#>  4: 1.7187315   1    1
#>  5: 1.3896163   1    2
#>  6: 1.5858805   1    2
#>  7: 1.4697276   1    2
#>  8: 1.9493473   1    2
#>  9: 1.5397020   1    3
#> 10: 1.2436558   1    3
#> 11: 0.8752505   1    3
#> 12: 0.9932352   1    3
#> 13: 3.1149370   2    4
#> 14: 2.7402102   2    4
#> 15: 2.4825228   2    4
#> 16: 2.8192831   2    4
#> 17: 2.8924475   2    5
#> 18: 2.8622759   2    5
#> 19: 2.8410755   2    5
#> 20: 3.0183753   2    5
#> 21: 2.6576575   2    6
#> 22: 2.0839150   2    6
#> 23: 2.2310707   2    6
#> 24: 2.3464027   2    6
#>          area CO2 tree

\[ y_i = CO2 * α_j + tree * β_k + ǫ_i \]

其中i代表第i个观测数据，j代表CO2浓度，k代表树。

m1 <- lm(area ~ CO2 + tree, stomata)
m0 <- lm(area ~ CO2, stomata)
anova(m0, m1)

#> Analysis of Variance Table
#> 
#> Model 1: area ~ CO2
#> Model 2: area ~ CO2 + tree
#>   Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
#> 1     22 2.1348                                
#> 2     18 0.8604  4    1.2744 6.6654 0.001788 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

通过anova方差分析可以看到，tree对气孔的影响显著。

m2 <- lm(area ~ tree, stomata)
anova(m2, m1)

#> Analysis of Variance Table
#> 
#> Model 1: area ~ tree
#> Model 2: area ~ CO2 + tree
#>   Res.Df    RSS Df  Sum of Sq F Pr(>F)
#> 1     18 0.8604                       
#> 2     18 0.8604  0 2.2204e-16

m2和m1的方差分析显示，CO2对气孔的影响也显著。CO2、tree对气孔是协同影响。

st = stomata[, .(area = mean(area)), .(tree, CO2)]
st

#>    tree CO2     area
#> 1:    1   1 1.623374
#> 2:    2   1 1.598643
#> 3:    3   1 1.162961
#> 4:    4   2 2.789238
#> 5:    5   2 2.903544
#> 6:    6   2 2.329761

m3 <- lm(area ~ CO2, st)
summary(m3)

#> 
#> Call:
#> lm(formula = area ~ CO2, data = st)
#> 
#> Residuals:
#>       1       2       3       4       5       6 
#>  0.1617  0.1370 -0.2987  0.1151  0.2294 -0.3444 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   1.4617     0.1629   8.970 0.000855 ***
#> CO22          1.2125     0.2304   5.262 0.006247 ** 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.2822 on 4 degrees of freedom
#> Multiple R-squared:  0.8738, Adjusted R-squared:  0.8422 
#> F-statistic: 27.69 on 1 and 4 DF,  p-value: 0.006247

# anova(m3)

summary(m3)$sigma^2 - summary(m1)$sigma^2 / 4

#> [1] 0.06770177

2.2 案例2

library(nlme)

data(Machines)
Machines %<>% data.table()

summary(Machines)

#>  Worker Machine     score      
#>  6:9    A:18    Min.   :43.00  
#>  2:9    B:18    1st Qu.:52.42  
#>  4:9    C:18    Median :61.60  
#>  1:9            Mean   :59.65  
#>  3:9            3rd Qu.:65.30  
#>  5:9            Max.   :72.10

head(Machines)

#>    Worker Machine score
#> 1:      1       A  52.0
#> 2:      1       A  52.8
#> 3:      1       A  53.1
#> 4:      2       A  51.8
#> 5:      2       A  52.8
#> 6:      2       A  53.1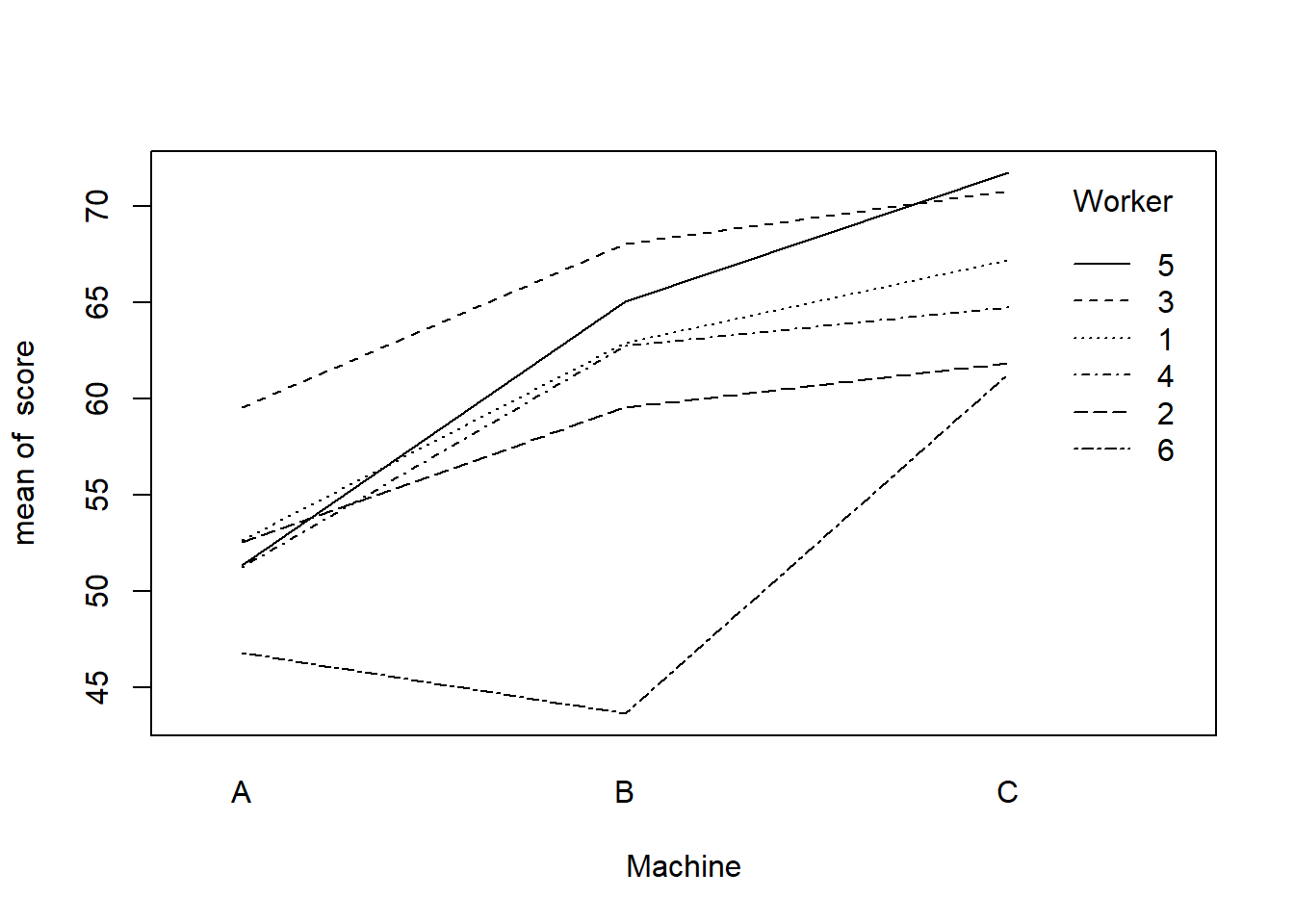

attach(Machines)
interaction.plot(Machine, Worker, score)

llm <- function(theta, X, Z, y) {
  ## untransform parameters...
  sigma.b <- exp(theta[1])
  sigma <- exp(theta[2])
  ## extract dimensions...
  n <- length(y)
  pf <- ncol(X)
  pr <- ncol(Z)
  ## obtain \hat \beta, \hat b...
  X1 <- cbind(X, Z)
  ipsi <- c(rep(0, pf), rep(1 / sigma.b^2, pr))
  b1 <- solve(
    crossprod(X1) / sigma^2 + diag(ipsi),
    t(X1) %*% y / sigma^2
  )
  ## compute log|Z’Z/sigma^2 + I/sigma.b^2|...
  ldet <- sum(log(diag(chol(
    crossprod(Z) / sigma^2 + diag(ipsi[-(1:pf)])
  ))))
  ## compute log profile likelihood...
  l <- (-sum((y - X1 %*% b1)^2) / sigma^2 - sum(b1^2 * ipsi) -
    n * log(sigma^2) - 
    pr * log(sigma.b^2) - 
    2 * ldet - 
    n * log(2 * pi)) / 2
  attr(l, "b") <- as.numeric(b1) ## return \hat beta and \hat b
  -l
}

# 将常数项去掉n
ormal.lik2<-function(theta, y){
  mu <- theta[1]
  sigma2 <- theta[2]
  n = length(y)
  z = (y-mu)/sigma  # logl = -0.5*n*log(sigma^2) - (1/(2*sigma^2)*sum((y-mu)^2)) 
  logl = 
    -1 / 2 * n * log(2 * pi) - 
     1 / 2 * n * log(sigma2) - 
     (1 / (2 * sigma2)) * sum((y - mu)**2)
  # `-1 / 2 * n * log(2 * pi)`: 常数项
  # logl = - 1 / 2 * n * log(sigma2) - (1 / (2 * sigma2)) * sum((y - mu)**2)
  -logl
}

# https://cloud.tencent.com/developer/article/1542008